An asymptotic formula for this sum

 Clash Royale CLAN TAG#URR8PPP
Clash Royale CLAN TAG#URR8PPP
up vote
5
down vote
favorite
Let $X$ be a positive real number. Can someone help me by providing an asymptotic formula for this sum.
$$sum_n leq X, ; n, equiv, a modb logn,$$
where $a$ and $b$ are two coprime integers.
Thanks in advance.
nt.number-theory analytic-number-theory
add a comment |Â
up vote
5
down vote
favorite
Let $X$ be a positive real number. Can someone help me by providing an asymptotic formula for this sum.
$$sum_n leq X, ; n, equiv, a modb logn,$$
where $a$ and $b$ are two coprime integers.
Thanks in advance.
nt.number-theory analytic-number-theory
add a comment |Â
up vote
5
down vote
favorite
up vote
5
down vote
favorite
Let $X$ be a positive real number. Can someone help me by providing an asymptotic formula for this sum.
$$sum_n leq X, ; n, equiv, a modb logn,$$
where $a$ and $b$ are two coprime integers.
Thanks in advance.
nt.number-theory analytic-number-theory
Let $X$ be a positive real number. Can someone help me by providing an asymptotic formula for this sum.
$$sum_n leq X, ; n, equiv, a modb logn,$$
where $a$ and $b$ are two coprime integers.
Thanks in advance.
nt.number-theory analytic-number-theory
edited Aug 6 at 8:37
Carlo Beenakker
68.1k8154256
68.1k8154256
asked Aug 6 at 8:32
Khadija Mbarki
672312
672312
add a comment |Â
add a comment |Â
1 Answer
1
active
oldest
votes
up vote
9
down vote
accepted
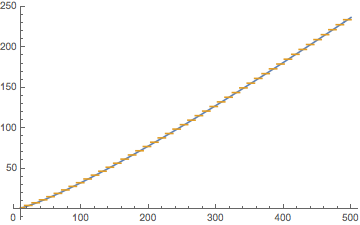
The sum
$$F(X)=sum_n leq X, ; n, equiv, a modb logn=sum_p=rm Int,[-a/b]^rm Int,[(x-a)/b]log(a+pb)$$
can be approximated in the large-$X$ limit by
$$F_infty(X)=sum_p=1^(X-a)/blog(pb)=fracX-ablog b+logGammaleft(fracX-ab+1right)$$
Here is a plot of $F(X)$ (gold) and $F_infty(X)$ (blue) for $a=5$, $b=11$.
add a comment |Â
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
up vote
9
down vote
accepted
The sum
$$F(X)=sum_n leq X, ; n, equiv, a modb logn=sum_p=rm Int,[-a/b]^rm Int,[(x-a)/b]log(a+pb)$$
can be approximated in the large-$X$ limit by
$$F_infty(X)=sum_p=1^(X-a)/blog(pb)=fracX-ablog b+logGammaleft(fracX-ab+1right)$$
Here is a plot of $F(X)$ (gold) and $F_infty(X)$ (blue) for $a=5$, $b=11$.

add a comment |Â
up vote
9
down vote
accepted
The sum
$$F(X)=sum_n leq X, ; n, equiv, a modb logn=sum_p=rm Int,[-a/b]^rm Int,[(x-a)/b]log(a+pb)$$
can be approximated in the large-$X$ limit by
$$F_infty(X)=sum_p=1^(X-a)/blog(pb)=fracX-ablog b+logGammaleft(fracX-ab+1right)$$
Here is a plot of $F(X)$ (gold) and $F_infty(X)$ (blue) for $a=5$, $b=11$.

add a comment |Â
up vote
9
down vote
accepted
up vote
9
down vote
accepted
The sum
$$F(X)=sum_n leq X, ; n, equiv, a modb logn=sum_p=rm Int,[-a/b]^rm Int,[(x-a)/b]log(a+pb)$$
can be approximated in the large-$X$ limit by
$$F_infty(X)=sum_p=1^(X-a)/blog(pb)=fracX-ablog b+logGammaleft(fracX-ab+1right)$$
Here is a plot of $F(X)$ (gold) and $F_infty(X)$ (blue) for $a=5$, $b=11$.

The sum
$$F(X)=sum_n leq X, ; n, equiv, a modb logn=sum_p=rm Int,[-a/b]^rm Int,[(x-a)/b]log(a+pb)$$
can be approximated in the large-$X$ limit by
$$F_infty(X)=sum_p=1^(X-a)/blog(pb)=fracX-ablog b+logGammaleft(fracX-ab+1right)$$
Here is a plot of $F(X)$ (gold) and $F_infty(X)$ (blue) for $a=5$, $b=11$.

edited Aug 6 at 8:55
answered Aug 6 at 8:48
Carlo Beenakker
68.1k8154256
68.1k8154256
add a comment |Â
add a comment |Â
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f307645%2fan-asymptotic-formula-for-this-sum%23new-answer', 'question_page');
);
Post as a guest
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password

